Building an Bayesian SMS sender
Mon Sep 16 2019tags: programming data science statistics multi-armed bandit bayesian inference behavioural economics project internship inzura public featured
I architected and built a system that programmatically sends SMSes and tracks each one to see if it has been clicked. I used the pipeline to conduct a behavioural economics experiment on ~2000 users to investigate the effect of loss-aversive framing on clickthrough rates. I used Bayesian statistics (Thompson sampling) to maximise the number of people who were reached by the optimal SMS.
I also sent various other SMSes (a total of ~10,000 messages). Overall, my interventions increased the number of active users by ~25% over a period of two months.
(Summer 2019 internship with Inzura)
As far as I am aware, this is the first behavioural economics experiment that uses Thompson sampling. There are very good reasons why most experiments don't (I elaborate upon this later), but I argue that the multi-armed bandit approach I used had several advantages over traditional A/B testing.
I had previously written a more technical post on Bayesian inference and Thompson sampling. Those interested in the details (or interested in picking apart my misunderstandings) are most welcome to peruse it. This post will talk about why I built the pipeline and the architecture of the pipeline, not the maths.
I have deliberately been vague about the details of the policy and campaign, to safeguard the privacy of our client.
Motivation
Our client is a large insurer who had rolled out a new policy that used our app. If the policyholder uses the app to record his driving (and fulfills some other conditions), he will be eligible for a cashback. However, people were not installing the app. Our working hypothesis was that people had either forgotten about the app, or had forgotten that they had to install it/use it to be eligible for a cashback. Therefore, we wanted to send reminder SMSes to these customers and see if we could get more uptake of the app.
As we were going into this blind, we wondered what sort of SMSes would be most effective. We decided to send three SMSes---a neutral reminder SMS, a "positive" SMS, and a "negative" SMS
Our purpose was twofold: i) to get as many people to install the app, and ii) to see which type of SMS was the most effective.
Why three types of SMSes?
Behavioural economics predicts that people are loss-averse: that is, they feel the pain of a loss more acutely than they feel the pleasure of an equivalent gain. My hypothesis was that an SMS worded to trigger loss aversion ("Install the app now or lose the cashback you're eligible for") would be more effective than an SMS worded positively ("Install the app now to gain a cashback"), which would in turn be more effective than a neutral reminder SMS ("Install the app now").
Why frame the experiment as a multi-armed bandit?
The gold standard of causal inference is to do a randomised controlled trial: randomly divide, say, 2400 participants into groups of 800 each, then send 800 the neutral (control), 800 the positive, and 800 the negative. Record the number of successes (clicked SMS) and failures (did not click SMS) for each treatment.
This is Good and Rigorous™. In particular, it maximises our certainty about the performance of each treatment. In most experimental contexts, this is fine. Most experiments try to uncover some fact about the world, and to maximise our certainty in the truth of those facts. But there are three additional considerations with this experiment design when it comes to the real world.
The first and biggest consideration is that nobody is going to let you run it because this is leaving money on the table. With this design 2/3rds (1600) of the customers will be getting a suboptimal SMS. In a business environment, we want to maximise the number of customers who receive the optimal SMS, not really maximise the certainty of our knowledge.
The second consideration is that we don't really want to be certain about the performance of every treatment. We want to be certain of the best treatment, which means that a uniform allocation (800 SMSes to each group) is nonideal. [1]
The third consideration is that we don't have to send all the SMSes at the same time. We can send a subset of the SMSes and use that initial data to draw tentative conclusions about which SMS is the best.
Given that we want to maximise the number of customers who receive the optimal SMS, the traditional experimental design is nonoptimal. But we don't know which SMS is best, so how do we find out as quickly as possible, and then maximise the number of customers who receive it?
It turns out that this problem can be neatly modeled as a "multi-armed bandit":
You are walking around the casino floor where there are ten slot machines, each with a different probability of paying out. How should one pull the slot machines in order to maximise one’s payout over the long run?
In this case, we have three slot machines (neutral, positive and negative SMSes). And since we don't know which arm is best, we have to send some SMSes initially to find out.
But there's a balance to be struck here. We want to spend some time learning, but after we're "pretty sure" about what the best arm is, we should keep pulling the best arm all the time. This is known as the explore vs exploit tradeoff (or, more pithily, "learn or earn"). We can see now why the initial experiment design was not fit for purpose: it's very good at learning, but no good at earning. (And we're trying to earn money here!)
Why Thompson sampling?
There are many proposed algorithms to solve the multi-armed bandit problem: these include epsilon-greedy, upper confidence bounds (UCB) and Thompson sampling.
I spent about a week reading the literature and thinking about it and eventually decided on Thompson sampling. More details are covered in my more technical post.
Experiment design
I decided on the following three SMSes (neutral, positive and negative):
You have not logged any trips. The <POLICY> you have purchased requires you to log trips regularly on the <APP> app. Install the app and start logging your trips today. Any problems, call <NUM>, or email <EMAIL>. Click here to start: http://<*>.inz.ai/<SMS_ID>
You have not logged any trips. The <POLICY> you have purchased requires you to log trips regularly on the <APP> app. Install the app and start logging your trips today to be eligible for your (up to) <AMT> cashback! Any problems, call <NUM>, or email <EMAIL>. Click here to start: http://<*>.inz.ai/<SMS_ID>
You have not logged any trips. The <POLICY> you have purchased requires you to log trips regularly on the <APP> app. Install the app and start logging your trips today or you will lose your (up to) <AMT> cashback! Any problems, call <NUM>, or email <EMAIL>. Click here to start: http://<*>.inz.ai/<SMS_ID>
While traditional multi-armed bandits allow you to pull one arm at a time and wait for the results, we didn't have the luxury of time here. Here we have to send thousands of SMSes in a short period of time, and we can't wait for the result of an SMS to come in (a user might take days to click an SMS if at all) before sending the next one. The simplest way is to simply send more SMSes in one go, but I wasn't sure if this would affect any of the nice guarantees (e.g. regret bounds) of Thompson sampling. I tried asking StackExchange but got no response.
I had to push through in any case. The modified Thompson sampling procedure works as follows. I start by sending a total of 300 SMSes per batch: in expectation, 100/100/100 of each type. Some of these SMSes will be clicked on and some will not.
Once the results come in, the algorithm will preferentially choose to send more of the better-performing SMS and fewer of the worst-performing one. For instance, after the first round the algorithm might send 124/80/96.
As more batches are sent, the algorithm builds up a better and better picture of the relative efficacy of each SMS, and will converge upon sending the best SMS exclusively.
In this experiment I sent 6 batches of SMSes.
Architecture
I knew what SMSes I wanted to send; I now had to build a system that would allow me to send it.
There are four key parts of this pipeline:
- Inzura server that contained customer data
- NGINX server to log clicked SMSes
- PostgreSQL database to log customer data and status of all SMSes sent
- Multi-armed-bandit code to calculate the optimal number of each SMS to send
I logged clicked SMSes in the following way:
SMS tracking architecture
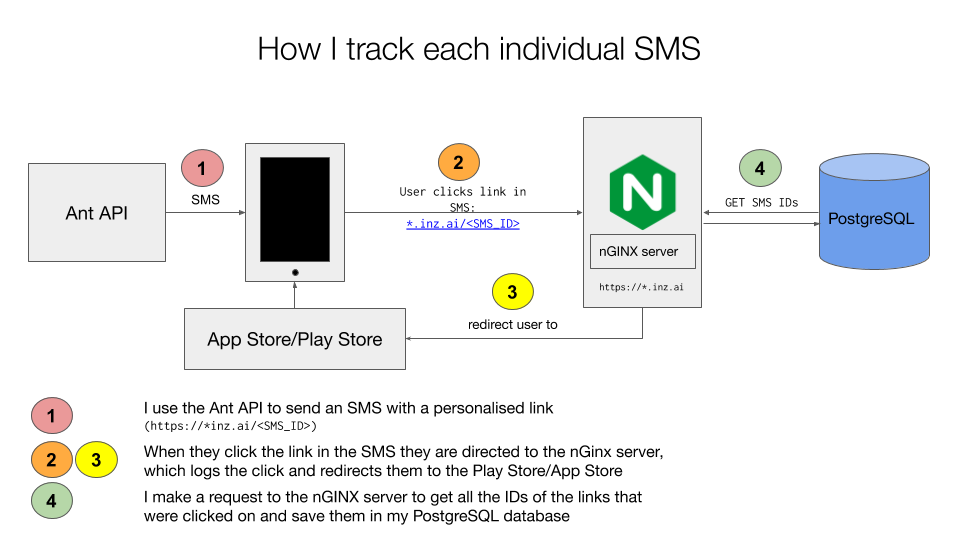
Step 1: The most important part is to measure the effectiveness of each SMS variant (neutral, positive or negative). I generate unique SMS IDs (3 alphanumeric characters + checksum) for each SMS and append them to a template string, making a unique SMS string. I then make GET requests to the service that sends SMSes, the Ant API.
Step 2 and 3: The user receives an unique SMS with a link at the end. Upon
clicking it, the user is taken to a logging server on the inz.ai domain,
which logs the ID of the SMS and redirects the user to the app store.
Step 4: I download the server's logs and process it, and update my database of which SMSes have been clicked.
Data analysis and MAB architecture
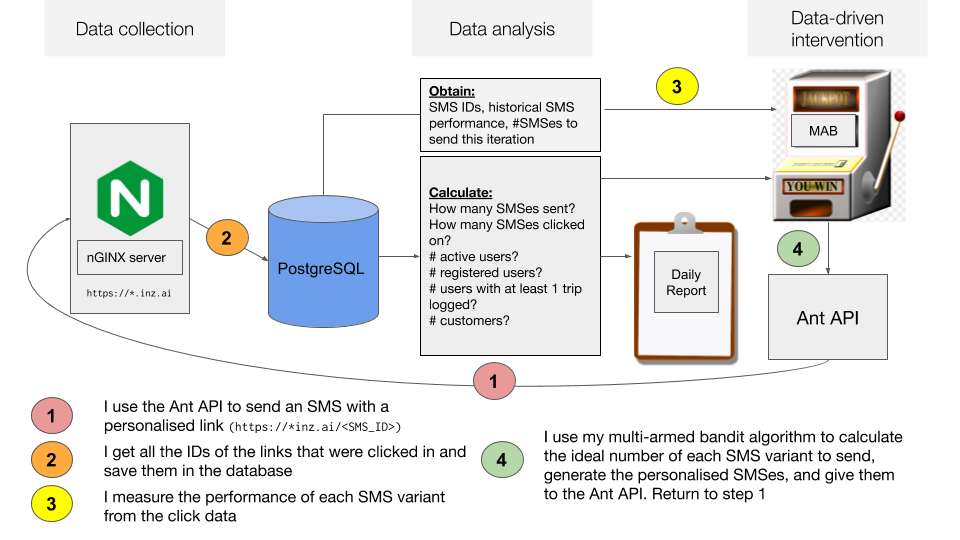
Now that I had a system to log SMS clicks, I had to implement the experiment.
First I had to create a PostgreSQL database and decide upon the schema for it.
Secondly, I had to pull customer data from the Inzura server and add it to the PostgreSQL database to identify eligible customers (we obviously don't want to send reminder SMSes to customers who have already installed the app).
Third, I had to write the Thompson sampling code that would read the data from the database (the slot machine labeled "MAB"). It calculates the optimal number of each SMS to send given the SMSes' past performances.
Finally, we generate unique SMSes and give them to the Ant API, and the cycle restarts. I call this a "pipeloop" because it's a pipeline that loops upon itself.
Thompson sampling code
This is the code that performs Thompson sampling. First, some definition:
Each arm is a tuple of the number of clicks and no-clicks of each SMS plus one. For instance, if I had sent 100 SMSes and there were 7 clicks, then the arm would be (8, 94).
The code takes a tuple of arms e.g. [(8, 94), (15, 87), (2, 103)] and the
number of samples we want to take (ergo the number of SMSes we want to send
this batch). It will then give us the optimal number of each SMS to send. In
the example above, the algorithm will tell us to send more of the 2nd SMS, some
of the 1st SMS, and almost none of the 3rd.
'''
Thompson sampling code
'''
from collections import namedtuple
import numpy as np
import random
from iteround import saferound
Arm = namedtuple('Arm', 'alpha beta')
def thompson_sample(arms, N):
'''
Takes as input arms and number of pulls we need to make, and
returns a tuple of arms to pull
'''
samples = []
arms_to_pull = []
for n in range(N):
samples.append([])
for arm in (arms):
samples[-1].append(sample(arm))
# pick the best arm
arm_to_pull = samples[-1].index(max(samples[-1]))
arms_to_pull.append(arm_to_pull)
return arms_to_pull
def sample(arm):
return np.random.beta(arm.alpha, arm.beta)Results
I got a null result. There wasn't much of a difference between loss-aversive SMSes (negative framing), positive SMSes and neutral SMSes.
Because we are using Bayesian statistics here, we can calculate the probability that loss-aversive SMSes are more effective than neutral or positive ones directly.
I calculated the following using a simulation approach:
There is a 26.6% probability that loss-aversive SMSes are more effective than neutral SMSes.
There is a 60.7% probability that loss-aversive SMSes are more effective than positive SMSes.
Obviously none of these results are very credible.
Code for the simulation:
import random
import numpy as np
def sample(tup, N):
return (np.random.beta(tup[0], tup[1], size=N))
N = 1000000
neutral = sample((69, 828), N)
positive = sample((10, 154), N)
negative = sample((19, 266), N)
c = list(zip(negative, neutral))
c = list(zip(negative, positive))
d = [1 for x in c if x[0] > x[1]]
print(sum(d) / N)The following diagrams are beta distributions. Think of them as a measure of our uncertainty in the effectiveness of each SMS. The x-axis measures the effectiveness of each SMS, and the y-axis measures our degree of certainty. The higher and sharper the distribution, the more certain we are about the effectiveness of an SMS.
The diagrams show the evolution of the estimates over time by SMS variant: red is neutral, green is positive, and blue is negative. Overall we can see that the distributions lie very closely to one another.
When we begin, we have no idea how effective the SMSes are, so we assume that
all SMSes form a uniform distribution. [2]

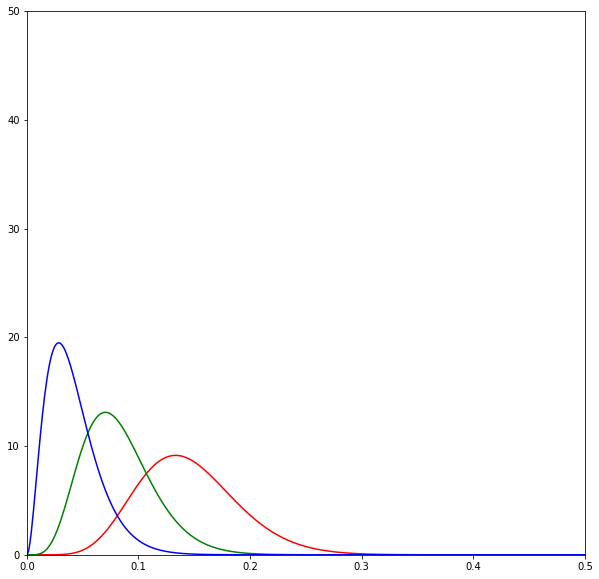
As we send SMSes and get the results back we begin to update our beliefs about the SMSes. Here the neutral SMSes seem to do best and thus the Thompson sampling algorithm chooses to send a lot of it.
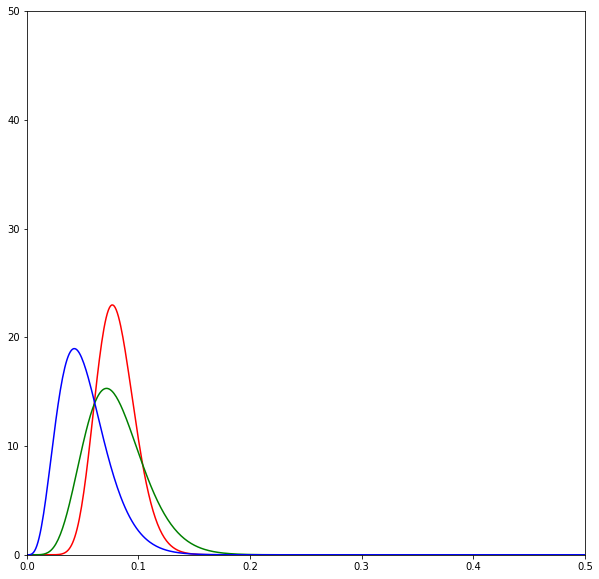
But the good performance of the neutral SMSes is quickly revealed to be a fluke as more SMSes are sent out.
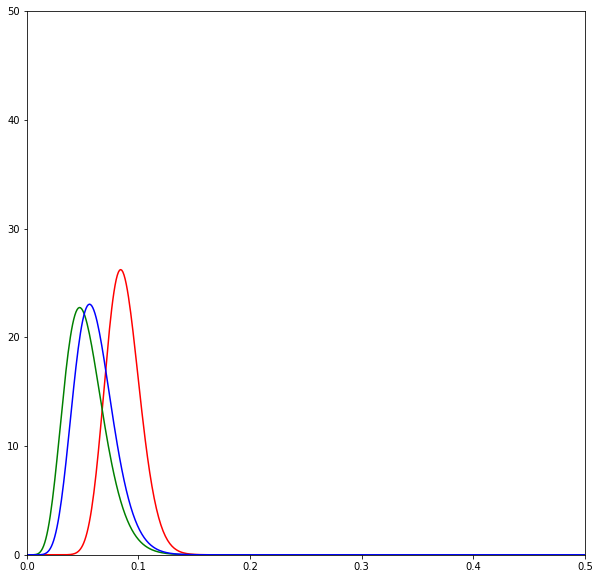
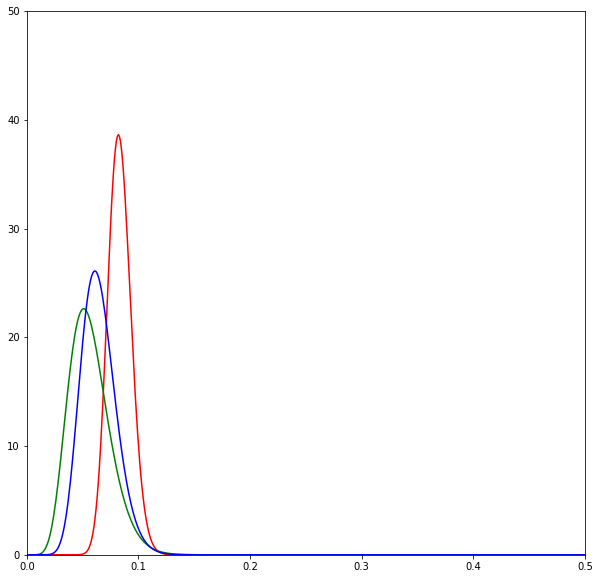
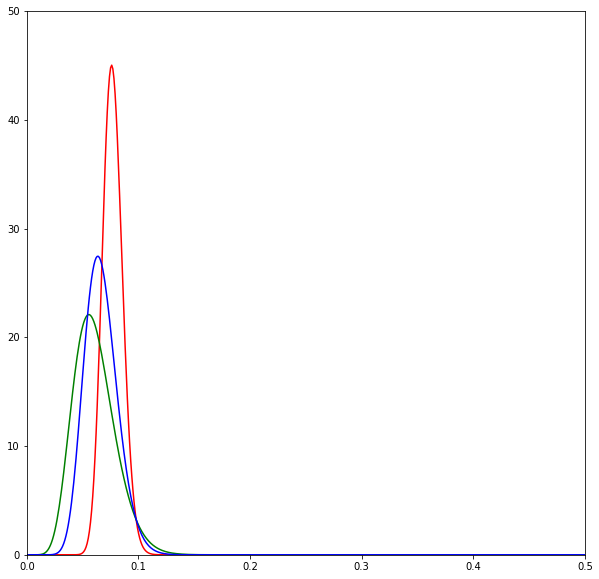
Eventually after all the SMSes have been sent we realise that all of the SMSes are about the same in effectiveness.
Due to time constraints, I could not run further experiments: I did A/B testing henceforth sending multiple reminder messages and again got null results. So I'm glad this was a very robust null finding :P
Nonetheless, my further interventions were able to increase the number of active users by around ~25%. I will not reveal numbers here for privacy reasons, but this had a real business impact because Inzura gets paid per monthly active user.
What I learned
I gained valuable practice in designing an experiment and carrying it to completion. I had originally wanted to kill two birds with one stone and use this for my BEE thesis, but a null finding isn't particularly exciting, so I will keep looking. [3]
I learned quite a lot about Bayesian inference in the course of designing the experiment, and would like to learn more about it. When I have more bandwidth I will consider doing the Probabilistic Graphical Models MOOC by Daphne Koller, and reading Judea Pearl's co-authored book on DAGs (highly recommended by Bassel).
I had to learn SQL in order to build the databases. In the course of doing this
project I worked through the Stanford Databases MOOC by Jennifer
Widom. I
completed DB1 Introduction and Relational Databases, DB4 Relational Algebra, DB5 SQL and DB8 Relational Design Theory. DB4 and DB8 helped me
design the schema and DB5 improved my very hackish/amateur queries into much
more elegant and readable ones.
Lastly, I was able to stretch my mind by architecting a complex system. It's kind of like thinking about the Lego parts you'll need to 3D-print to build the rocket ship you have in mind. It was a good exercise to think about what parts I needed in the system and how they would talk to each other. (I guess this is what senior SWEs like Chris and David do in their sleep.) I've greatly simplified the architecture in my breezy explanation---the actual architecture I built has more moving parts, and it was quite challenging for me.
Conclusion
I am very glad that my knowledge of statistics and behavioural economics could be brought to bear in this project. I have always gone through my degree thinking that it was useless for doing anything technical.
This project gave me an idea about my comparative advantage in data science. While it isn't difficult for a computer science major to learn statistics, many of them might not have done so. If I max out my statistics and maintain my ability to write software I could be some sort data-scientist data-engineer hybrid; not a "pure" data scientist but someone who likes to get his hands dirty wrangling the code and building the systems.
This is the problem of "best arm identification". For N > 2, it isn't optimal to pull all arms equally. If one arm is very obviously worse than the rest, the algorithm shouldn't waste time on pulling it more. this paper (Best Arm Identification in Multi-Armed Bandits) has more details. See also this paper on Heoffding and Bernstein races where the objective is to try to establish the best action at a given confidence level with the fewest pulls. ↩︎
The choice of a uniform prior was because I had never run an experiment like this before, and had no idea what the clickthrough rate of an SMS was supposed to be. For subsequent experiments I would initialise the priors at around a 0.07 click rate. ↩︎
Yes, I know I'm contributing to publication bias---but my grades are on the line here... ↩︎