Group testing to save the world

Sun Jan 24 2021

tags: public exploration maths computer science featured

The year is 2021. The world has been transformed into a post-apocalyptic wasteland. COVID-19 has been cured, but one of the vaccines went horribly awry: some of the people who got the Oxford-Zeneca vaccine started frothing at the mouth, indiscriminately biting people, and chanting "Volker Halbach, Volker Halbach" before succumbing to their lack of qualia.

Two back-to-back pandemics were too much for the world to handle, and the remnants of humanity have been reduced to scavenging for GrabFood discounts.

But there is hope. A new screening test has been devised: a perfect test that can detect for sure whether someone has the virus in a matter of seconds...

You are an overworked civil servant at the Ministry of Health. Your boss comes in one day brandishing a couple of important-looking documents.

"New directive from the Minister---we need to test every traveler that comes in to the country. Can you write me a proposal by today?"

What choice do you have? You get to work.

0. The basic one

The proposal goes something like this: All visitors to the country will line up at a testing booth. When it's their turn they'll spit in a cup and then their secretion will be tested for the virus. If they test negative, they're free to go; if they test positive, they're whisked away to a quarantine facility ~~never to be seen again~~. You bang it all out and send it to your boss.

How to test travelers

You get a call the next day. Your boss is aghast.

"We haven't got nearly enough tests to test everyone who comes!" he shouts.

"Can we order more tests?" you ask.

"No, the whole world is out of tests."

You take a deep breath to calm yourself.

"The Minister wants us to test everybody that comes in, right?"

"Yes."

"But we don't have enough tests to test everybody?"

"Yes."

A few choice words come to mind, but you (wisely) stay silent.

If your boss had any shame he'd have the courtesy to at least look sheepish, but unfortunately all senior civil servants have had that part of the brain surgically excised. In any case, he wants you to come up with a new proposal. "Can you find some way to test everyone, but with fewer tests? As few as possible?" You try to say something noncommittal but he's already hung up.

Clumps of your hair lie morosely on the table.

Testing everyone without enough tests for everyone? How is that possible?

You review the evidence. Preliminary findings suggest that out of every 1000 people, roughly 3 people will have the virus. Also, the test is perfectly accurate and infinitely-sensitive, which means that it always gives the right answer, and we can test as many people as we want with one test. (Since the test is infinitely-sensitive, you can test the tiniest drop of a person's spit, and it will give you the right answer).

Then you have a flash of insight:

Let's make one small change to the protocol. Visitors will have to queue-up-and-spit---just as before---but now TWO visitors will spit in one cup. This combined cup will then be sent for testing. Because the test is infinitely sensitive, it will test positive if either (or both) of the visitors have the virus. If the combined test comes back negative, then neither visitor has the virus, and they are free to go. If it comes back positive, then at least one of the pair has the virus. We then test each of them individually.

This two-visitors-one-cup protocol will save almost half of the tests because most of the tests will come out negative. Why is this so? The key here is that most travelers don't have the virus.

Let's use an example to illustrate.

Suppose we have 1,000 travelers and 3 of them have the virus. ^[1] If you test them individually then you will use up 1,000 tests. If you pair them up at random, however, one of the following must be the case:

There are three pairs with one positive person, and 497 all-negative pairs.
There is one pair with two positive people, one pair of one pair with one positive person, and 498 all-negative pairs.

In the first case, we will use 500 tests for each of the pairs. Three of those tests will come out positive and we will use an additional two tests for each of them. The total number of tests is $500 + 3*2 = 506$ .

In the second, we will again use 500 tests for each of the pairs, and use two additional tests for each of the two positive pairs, for a total of $500 + 2*2 = 504$ .

In either case, we've cut the number of tests needed by almost half! This method only works because most travelers are negative, and so most pairs will test negative. By contrast, if the infection rate was much higher and 800 out of every 1000 people had the virus then almost all of the pairs would test positive and you would do better just testing everyone individually.

If two is good, surely three is better, four even better, and ten double-plus-good better? We'll divide travelers into groups---of, say, ten--- and get them all to spit into the cup. Doing so could save us even more tests if most visitors don't have the virus. Assuming we only have three visitors with the virus out of our 1000 visitors, there can be at most three positive groups no matter the group size. Doing groups of 10 would mean at most thirty individual tests, for an upper bound of $100 + (3*10) = 130$ tests.

But of course, there's an upper bound to how many people you can put in a group. If you get all 1,000 people to spit into the same bucket (yucks) and test that you'll only have to do one combined test, but that test is definitely going to come out positive and you're going to have to test all 1,000 people individually. Then you haven't saved any tests at all.

We can calculate the optimal size for each group. The trade-off of having bigger groups is that you do fewer group tests that combine multiple people, but have to do more individual tests when a combined test comes back positive. Let's introduce some notation:

Number of total people = $N$
Number of infected = $K$
Number of groups = $G$
Number of people in each partition = $N/G = p$

In the worst case you have to do $G + (p * \min(K, G))$ tests.

Why is this so? In the first step you need to test the $G$ groups. And in the worst case, all $K$ of the groups will come out positive (ergo each positive group has exactly one positive person), and you'll have to test each of those $K$ groups individually which takes $p$ tests each.

We can prove by differentiation that the optimal number of people in each partition, $p^{*}$ , is given by $p^{*} = \sqrt{\frac{N}{k}}$ .

Using our example of $N=1000$ and $K=3$ , this would mean that the optimal group size is $\sqrt{333}$ which is something like 18.5. ^[2] If we use $p = 20$ instead (just so the numbers are easier to work with) you would need $50 + (3*20) = 110$ tests at most in the worst case, where you do 50 combined tests, then test the 3 positive groups of 20 individually.

That's quite a big reduction. By grouping people together into larger groups and testing those groups we can decrease the number of tests needed by almost 90%, from 1,000 to around 100.

You sketch out a diagram of how this larger group test approach works and email it to your boss. He makes a couple of quick scribbles on it and it's quickly distributed to Border Control:

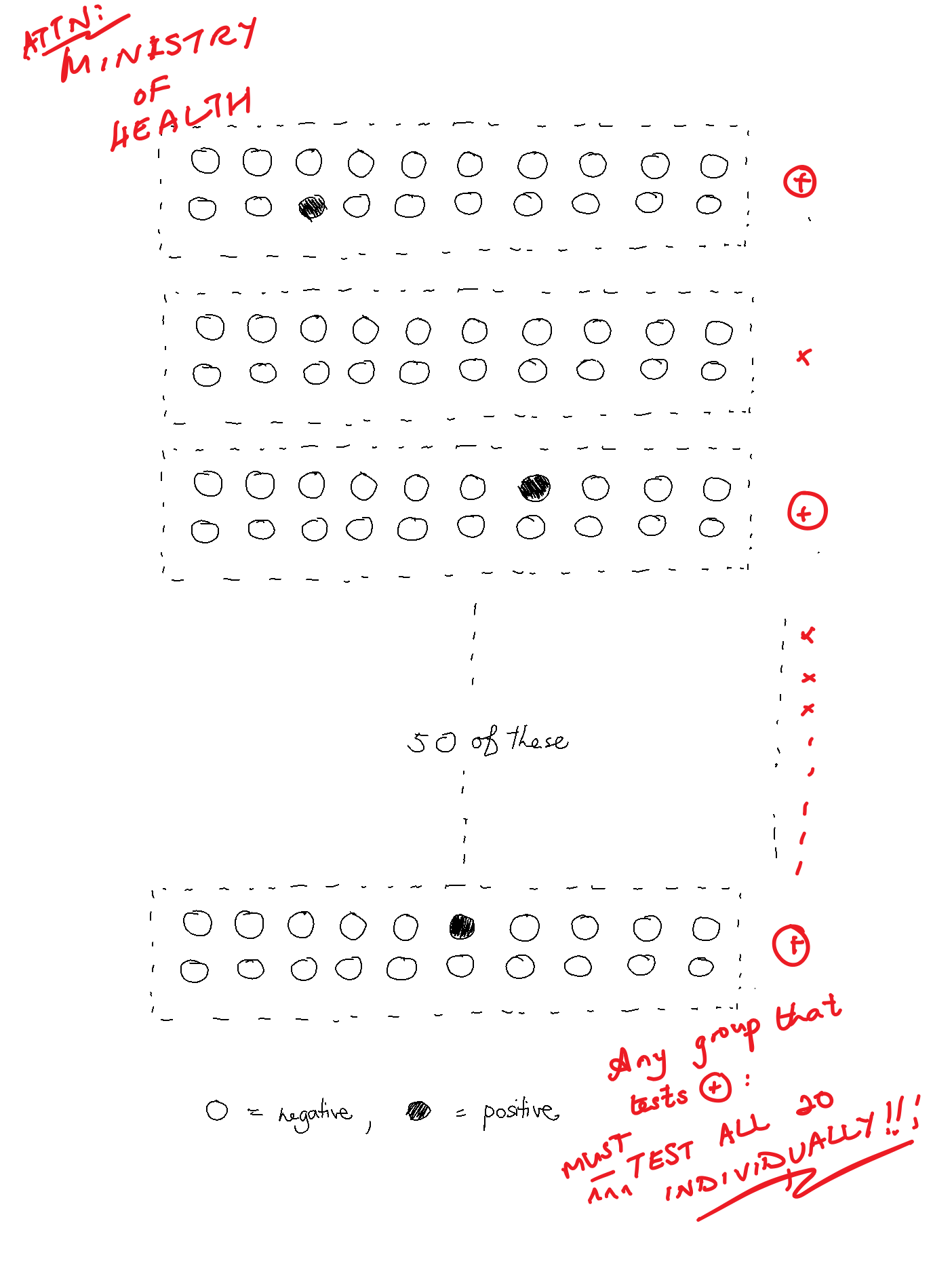
Handout to ministry workers

For a while, all is well. You've done the impossible with your great leap of insight and your boss gives you an A in your performance appraisal. Your meteoric rise through the ranks of the Civil Service is all but assured, you think to yourself -- but alas, Fate is never so kind...

A few months later, you enter the office and find it in a state of upheaval.

It is pandemonium. Your colleagues are screaming, jumping on desks, and smashing file cabinets: files and papers litter the floor, and your Director is bawling his eyes out.

"What happened here?" you ask, and in between racking sobs he points to a stack of papers on his desk:

As part of the Digital Government Blueprint and the continuing economic difficulties caused by the post-pandemic pandemic, we call upon the Whole-of-Government to embark upon a Productivity Improvement and Digitisation Journey to increase WoG efficiency and reduce government expenditure...

Lesser men would have gotten hopelessly lost in the thick thicket of Bureaucrat-ease, but you realise the subtext immediately. In order for your boss to keep his year-end bonus all his charges must demonstrate a 25% efficiency increase ---which means you have to reduce the number of tests by 25%.

(At this point the reader might wonder if a fairly mundane requirement of a efficiency increase could lead to such an exaggerated scene. I congratulate such a reader for his good fortune not to have worked in the Civil Service).

You steal a furtive glance at your boss. He seems to have recovered very quickly and is now eyeing you expectantly. You try to tell him that you've already saved him 90% of tests but he's having none of it. He quickly shoos you out of his office, leaving you once again to do the seemingly impossible...

Your most recent proposal is to test groups of 20. If any group's test comes back positive, test every single person in that group. But must we test everyone individually once a group tests positive? Can't we group people together again into subgroups of, say, 5? And if that subgroup tests positive, can't we group people together again? And so on. After all, if we were able to save tests by splitting our original group of 1000 into sub-groups, maybe we can save even more tests by splitting our sub-groups into sub-subgroups etc.

Here's an example. We have a group of 20 that tested positive. We might then choose subgroups of 5 from that 20, and start testing the first subgroup of 5. If that subgroup tests positive we then split them again into sub-subgroups of 2 and 3, and if those sub-subgroups test positive we test them individually. As before, if any group/subgroup/subsubgroup... tests negative then we simply move on to the next one.

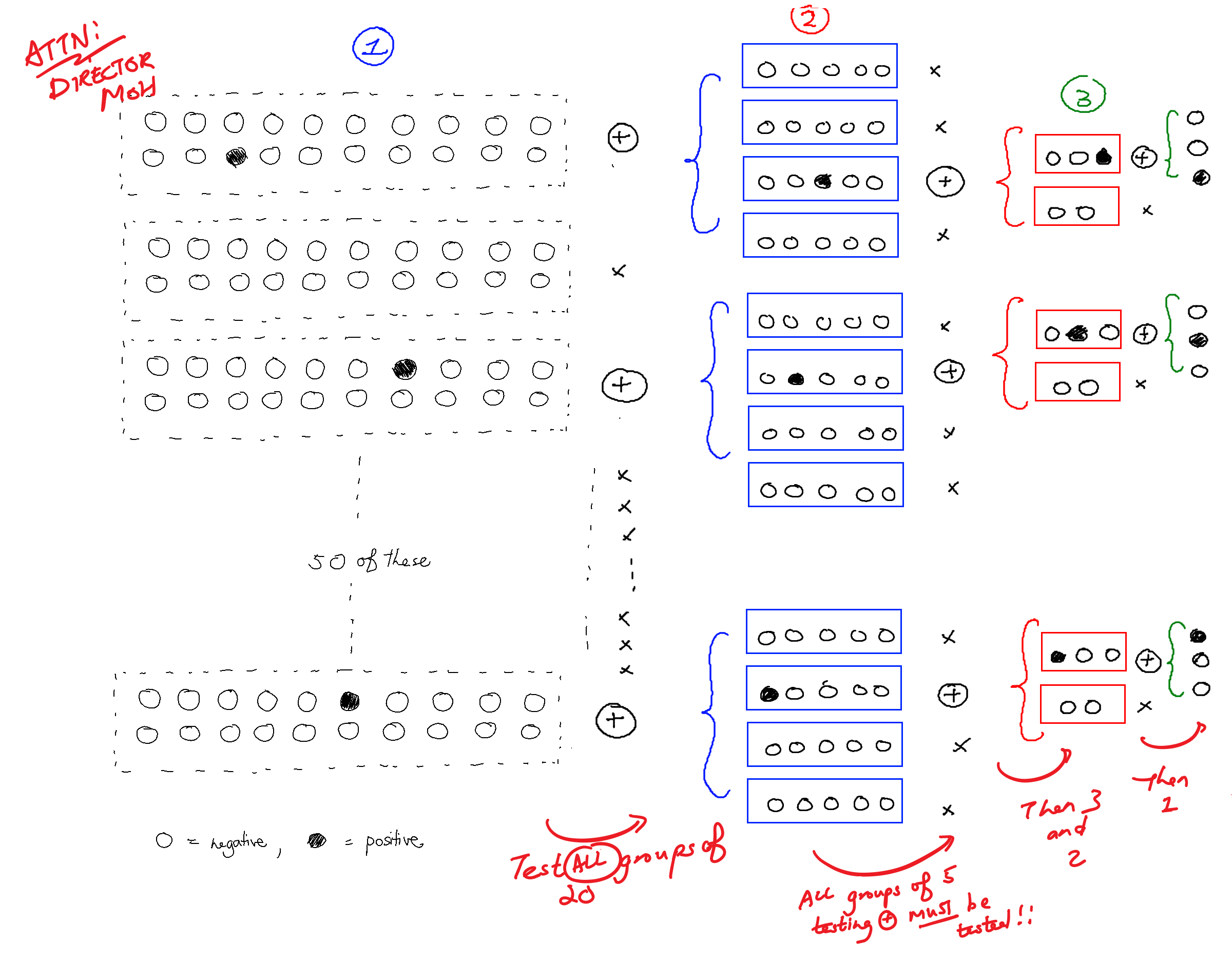
Breadth-first search

Does this actually save us tests? Let's think about how many tests we would use in the worst case. The worst case is when the positive tests are as "spread out" as possible: that is, in different groups/subgroups/sub-subgroups.

So we test 50 groups of 20, using 50 tests. In the worst case, three of the groups test positive.

When we get a positive group of 20 we split it up into subgroups of 5. There will be 12 such subgroups in total ( $(20 * 3)/ 5 = 12$ ). We test all 12, using 12 tests. In the worst case, three of those subgroups test positive.

Again, when we get a positive subgroup of 5 we split them up into sub-subgroups of 2 and 3. There will be three subgroups of 2 and three subgroups of 3.

Again we test all six, using 6 tests. Three of those sub-subgroups test positive, and because this is the worst case, all the positive sub-subgroups are of size 3.

Finally, we test each of those sub-subgroups individually, using $3*3 = 9$ tests, for a total of $50 + 12 + 6 + 9 = 77$ tests.

You've saved the day again! You send the improved proposal to your boss and pat yourself on the back for a job well done. You quickly update your Tinder profile: after all, nothing gets women more excited than "Achieved process improvements of more than 90% for the Ministry of Health".

But while things are still fresh in your head ---and knowing that your boss will probably try to squeeze more out of you--- you reckon that you should keep thinking of more improvements to continually dole out. You wouldn't want work to get in the way of your schmoozing, after all. So you keep cracking...

4. Can we do better by picking the right sub/subsubgroup size?

You know from part 2 that choosing the right group size makes a pretty big difference in the number of tests we need. It stands to reason that the subgroup and subsubgroup sizes also matter. But how should we pick these sizes? In part 2 we calculated the optimal group size (20) but in part 3 we picked the subgroup sizes arbitrarily (sizes 5 and 2). Can we do better?

It turns out that we should halve the size of the (sub)group each time.

Concretely, we start with a group size of 20 and first conduct a test on the first 10 of the 20 people (i.e. the subgroup size is 10), allowing us to eliminate either these 10 people (if the test came back negative) or the other 10 people (if the test came back positive). But what if both subgroups of 10 test positive? Given the small number of positive cases, the odds of getting two or more positive elements in a group of 20 are very low, so in the vast majority of cases we will eliminate half of the people. (But see a more rigorous treatment in the Appendix!)

After the first test 10 people remain. We conduct a test on the first 5 of the 10 people (subgroup size 5), allowing us to eliminate 5 people. We continue doing so until we are left with a single person --- this person must be infected. This is an idea very similar to binary search. (The proof of why binary search is optimal can be found in the Appendix).

5. Can we do better by picking the right group size (again)?

We previously showed in part 2 that the ideal number of people in each group is $p = \sqrt{\frac{N}{k}}$ . However, that calculation hinges on the assumption that there is only one level of grouping before we test each person individually. This isn't the case now, since we have many levels (specifically it's $\log_2 \frac{N}{p}$ levels, since we halve the number of people in a (sub)group after each test).

What is the new ideal group size $p$ ? Because we halve the size of the group each time, we need (at most) $\log_2 \frac{N}{p} + 1$ tests per infected individual. And since there are $k$ infected individuals, we need a total of $G + k (\log_2 \frac{N}{p} + 1)$ tests: $G$ initial tests, then $\log_2 \frac{N}{p} + 1$ individual tests. Using differentiation we find that the optimal number of people in each partition, $p^{*}$ , is given by

p^{*} = \frac{N}{k}.

Note how it is the square of the previous value

p^{*}_{old} = \sqrt{\frac{N}{k}}.

Importantly, this new group size is larger than the previous group size, which makes a lot of intuitive sense. Remember that the fundamental group size trade-off is that if you make your group size too large, you will expend a lot of tests testing every one individually (subgroups of 1). But in our refinements of the method we have managed to use fewer tests by choosing the right subgroup size. The optimal group size therefore increases. (And for our case of $N = 1000$ and $k = 3$ , the optimal group size is $p^{*}=333$ ).

6. Depth-first search: should we "reset" the search after we've found an infected person?

Previously, we were testing all 50 groups of 20 before testing the 12 groups of 5, and testing all the 12 groups of 5 before testing the 6 groups of 2 or 3.

There is another way to do it, though. We could test groups of 20 until we find a group of 20 that tests positive. Once we find a positive group of 20 we test groups of 5 from that 20 until we find a group of 5 that tests positive, and from that group test the groups of 2 and 3, and so on. Only when we find an infected individual do we go back up a level.

Here's an illustration of what that looks like:

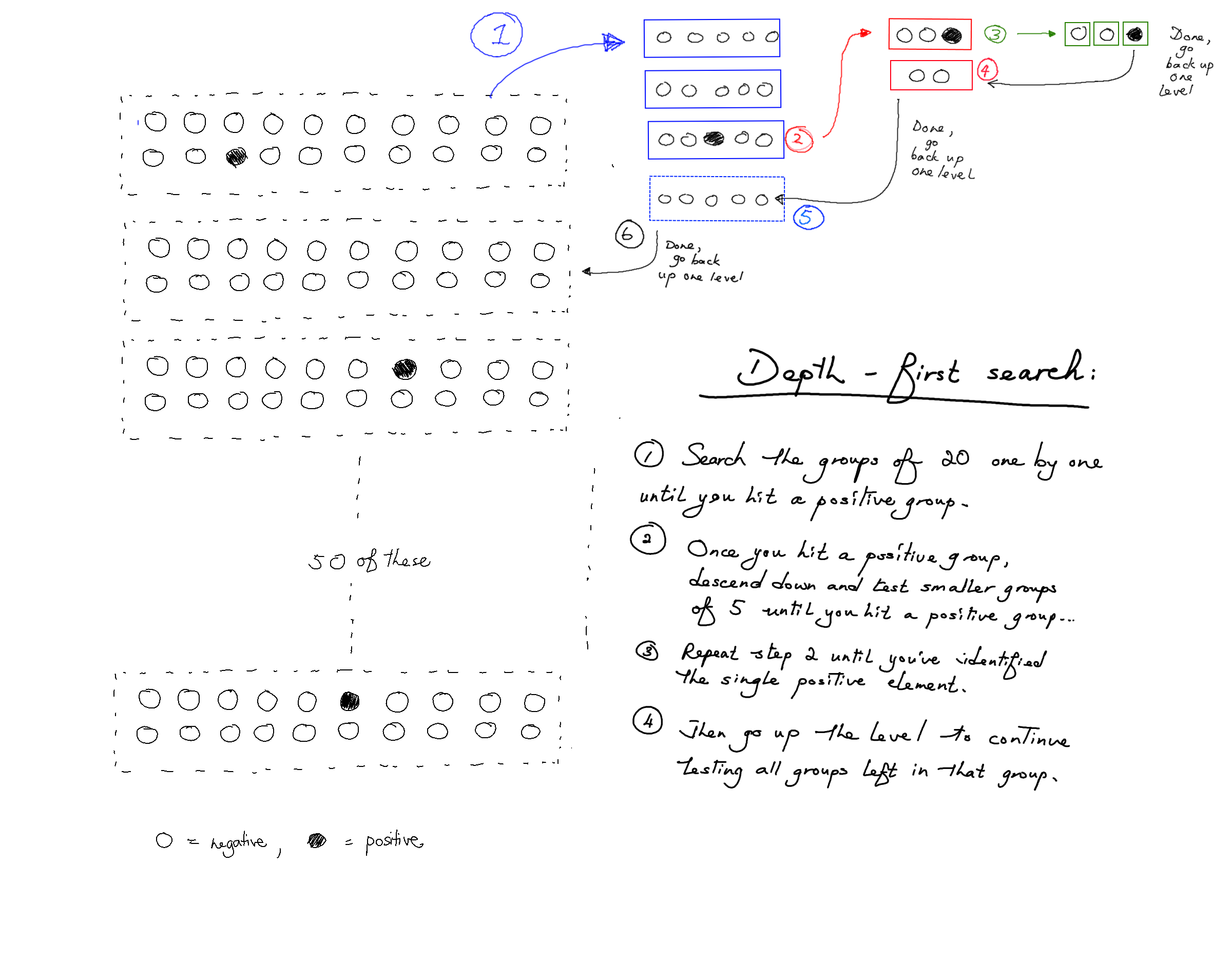
Depth-first search

This is called breadth- vs depth- first search. In breadth-first search, we explore all groups of the same size before exploring groups of smaller sizes (i.e. deeper levels). But in depth-first search, we make our way to the first infected person as quickly as possible, before backtracking to find the next infected person, and so on.

Does it matter whether we use depth- or breadth-first search? It turns out that depth-first search opens up some further optimisations. The idea is that once we find the first infected individual we can stop and "reset" the search, using fewer tests overall.

Suppose we conduct our tests, using the depth-first search procedure, pausing just after we have identified the first infected individual (in our example, it is the 13th person). But note here that we have no information whatsoever about the people behind the 13th person. More specifically, we know that persons 1 to 12 are not infected, and (of course) that person 13 is infected, but we don't know anything about whether any of the subsequent people are infected. This is because subsequent infected people don't affect any of the test results obtained so far by the procedure. This means that persons 14 to N are as likely to be infected as any other person we haven't tested: it is as if we never did any tests on them at all.

In our current procedure, after finding that the 13th person is infected, we backtrack and test the 14th and 15th persons together (size 2) then back out further and test the 16th to 20th person (size 5). But if you think about it, since persons 14 to 20 are as likely to be infected as any other person we haven't tested, we have no information about the 14th to 20th people, and as such have no reason to test them in small groups. You can think of it like the 13th person being positive "polluted" the group test of 20 people.

For this reason, if you did actually test the groups [14, 15] and [16, 20], both two tests will very likely be negative! And this is inefficient: it's similar to doing individual testing when we know that most people will test negative.

What should we do, then? The key insight here is to "reset" the search. Since persons 14 to N are equally likely to be infected, we arrive at a smaller instance of the same original problem --- there are $1000-13=987$ people that we want to test, of which $3-1 = 2$ of them are infected! It then follows that we should perform an identical procedure on these remaining people --- we recalculate the new value of $G$ (and hence $p^{*}$ ), and proceed with the procedure with those new values.

All the optimisations lead you to the final, optimal algorithm:

Set the optimal group size as $p = N/k$ . Pick the first $p$ people, group them together and test them.
If that group tests negative, remove all of these people, and repeat the algorithm with $N$ now set to $N-p$ .
If that group tests positive, take a subgroup of the first half of those people and test them:
- If that subgroup tests negative, clear them and test the first half of the other subgroup.
- If that subgroup tests positive, test the first half of the subgroup.
- In either case, repeat this process until we get to a single person.
Remove all the people before and including the first positive person, repeating the algorithm and setting $N$ and $k$ appropriately. Repeat this process until everyone has been cleared or quarantined.

You smugly file the optimal algorithm away, content in the knowledge that you'll be able to appease your boss and exceed your KPIs for many months to come. You're feeling very clever with yourself, but unbeknownst to you Hwang (1972) beat you to it almost fifty years ago with his paper A Method for Detecting All Defective Members in a Population by Group Testing (maybe you should have studied something useful instead of PPE). Over the next few months you spend your working hours writing florid poetry on the human condition, slowly moulding yourself into the Tang dynasty bureaucrat-poet all AOs surely aspire toward becoming.

THE END

Conclusion

In this post we went through Hwang's 1972 algorithm, which allows us to find all the people who test positive for a disease using only a small number of tests.

We kickstarted our intuition by realising that we can group people and test them together. If the number of positive people is small most of these groups will come back negative (and thus no further testing is necessary). This gave us a large decrease in the number of tests needed.

We further improved the method by noting that i) we can split groups into subgroups, sub-subgroups etc. when a group tests positive, and ii) the best way to split a group that tests positive is into two groups of half the size.

Finally, we showed that we simply arrive at a smaller instance of the same original problem once we find a positive person, and it is optimal to simply "reset" the search with smaller values of $N$ and $k$ rather than continue to split the groups/subgroups in the original search.

There are a few possible extensions to this piece. For instance, what if tests are noisy (they sometimes give false positives/negatives)? Then you can never have certainty, only a certain posterior probability. Also, this algorithm runs serially, not in parallel. You have to wait for the results of the group tests before testing the subgroups. What if (due to time constraints) you're not allowed to do that? Is there a better algorithm? What if you're allowed to do at most e.g. 3 rounds of tests? Can we find an algorithm that allows us to specify a tradeoff between the number of test kits needed verus the number of "rounds" of tests? Please let me know if you are interested in reading posts on these extensions, or have any suggestions for improvement.

Acknowledgements

I worked on this piece together with Bernard Teo Zhi Yi. The idea for this post came from Bernard, who is currently writing his thesis on group testing. He is very much the brains behind this piece.

A big thanks to Robert Heaton for reading a draft of this work and providing very valuable comments. Thanks also to CKY, Ed, Nick, Celine, Wilfred, and Joy for reading early drafts of this piece and giving me helpful comments.

Appendix

Why halving the group size each time is optimal

Each group that tests positive is quite likely to have only one infected individual, because there are more groups than infected individuals. Suppose you rolled twenty 100-sided dice (d100): the odds of getting one 100 is quite rate, but the odds of getting two or more 100s is vanishingly unlikely. In the same way, since an individual is very unlikely to have the virus, it is quite rare for a group to have an infected person, and extremely rare for a group to have two (or more) infected people.

Let's assume for now that each group that tests positive has exactly one infected individual. Our objective, then, is to determine which one of the 20 people in this group is infected with the minimum number of tests, and this is optimally done by halving the group size each time.

To see why halving the group size each time consider what would happen if we first conducted a test on 5 (instead of 10) of the 20 people in the group. If the test comes back positive, then we get to eliminate a whopping 15 people! But if the test comes back negative, then we can only eliminate 5 people. On average, then, what is the number of people that we will get to eliminate?

If you've answered "10 people", that's unfortunately wrong. Since the infected individual has an equal chance of being each of the 20 people in the group, it is more likely that the the infected individual is in the untested 15 remaining people rather than the 5 people we conducted a test on. This means that it's more likely that we will only get to eliminate 5 people, rather than 15. As such, the average number of people that we get to eliminate is less than 10.

We may make a similar argument if 15 people are chosen for the first test, instead of 5 or 10. The average number of people that we get to eliminate will also be less than 10.

Hence, testing exactly half of the group is the most efficient way to narrow down the group size.

Note that this method doesn't rely on knowing exactly how many people have the virus, only the expected value. If you knew that there were EXACTLY three people you could stop once you found three positives. For ease of exposition we illustrate an example where there are exactly 1,000 travelers and exactly 3 positive cases, but the method and the probabilities are very similar even if we work with expected values instead. ↩︎
You can achieve an effective group size of 18.5 by having groups of 18 and 19. ↩︎